Influence of an inner core on the long-period forced librations of Mercury,

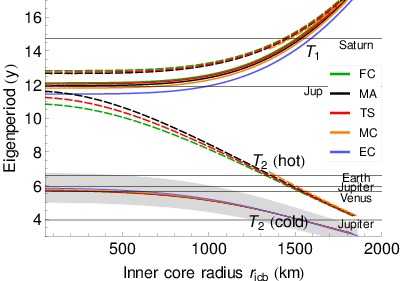
The free modes of Mercury if there is a solid inner core

 The planetary perturbations on Mercury's orbit lead to long-period forced librations of Mercury's mantle. These librations have previously been studied for a planet with two layers: a mantle and a liquid core. Here, we calculate how the presence of a solid inner core in the liquid outer core influences the long-period forced librations. Mantle-inner core coupling affects the long-period libration dynamics mainly by changing the free libration: first, it lengthens the period of the free libration of the mantle, and second, it adds a second free libration, closely related to the free gravitational oscillation between the mantle and inner core.
The two free librations have periods between 2.5 and 18 y depending on the internal structure. We show that large amplitude long-period librations of 10's of arcsec are generated when the period of a planetary forcing approaches one of the two free libration periods.
These amplitudes are sufficiently large to be detectable by spacecraft measurements of the libration of Mercury. The amplitudes of the angular velocity of Mercury's mantle at planetary forcing periods are also amplified by the resonances, but remain much smaller than the current precision of Earth-based radar observations unless the period is very close to a free libration period.
The inclusion of mantle-inner core coupling in the rotation model does not significantly improve the fit to the radar observations.
This implies that it is not yet possible to determine the size of the inner core of Mercury on the basis of available observations of Mercury's rotation rate. Future observations of the long-period librations may be used to constrain the interior structure of Mercury, including the size of its inner core.


Yseboodt, M., A. Rivoldini, T. Van Hoolst and M. Dumberry,
Influence of an inner core on the long-period forced librations of Mercury,
Icarus, Vol 226, p41-51, 2013.

Analytical model of the long-period forced longitude librations of Mercury


The shaking of Mercury’s orbit by the planets forces librations in longitude in addition to those at harmonics of the orbital period that have been used to detect Mercury’s molten core. We extend the analytical formulation of Peale et al. (Peale, S.J., Margot, J.L., Yseboodt, M. [2009]. Icarus 199, 1–8) in order to provide a convenient means of determining the amplitudes and phases of the forced librations without resorting to numerical calculations. We derive an explicit relation between the amplitude of each forced libration and the moment of inertia parameter B-A/Cm. Far from resonance with the free libration period, the libration amplitudes are directly proportional to B-A/Cm. Librations with periods close to the free libration period of ~12 years may have measurable (~arcsec) amplitudes. If the free libration period is sufficiently close to Jupiter’s orbital period of 11.86 years, the amplitude of the forced libration at Jupiter’s period could exceed the 35 arcsec amplitude of the 88-day forced libration. We also show that the planetary perturbations of the mean anomaly and the longitude of pericenter of Mercury’s orbit completely determine the libration amplitudes. While these signatures do not affect spin rate at a detectable level (as currently measured by Earthbased radar), they have a much larger impact on rotational phase (affecting imaging, altimetry, and gravity sensors). Therefore, it may be important to consider planetary perturbations when interpreting future spacecraft observations of the librations.


Yseboodt M., Margot J.L. and Peale S. J.,
Analytical model of the long-period forced longitude librations of Mercury,
Icarus, Vol 207, doi: 10.1016/j.icarus.2009.12.020, 2010.

Resonant forcing of Mercury's libration in longitude


The period of free libration of Mercury's longitude about the position it would have had if it were rotating uniformly at 1.5 times its orbital mean motion is close to resonance with Jupiter's orbital period. The Jupiter perturbations of Mercury's orbit thereby lead to amplitudes of libration at the 11.86 year period that may exceed the amplitude of the 88 day forced libration determined by radar. Mercury's libration in longitude may be thus dominated by only two periods of 88 days and 11.86 years, where other periods from the planetary perturbations of the orbit have much smaller amplitudes.


Peale S. J., Margot J.L. and Yseboodt M.,
Resonant forcing of Mercury's libration in longitude,
Icarus, Vol 199, Pages 1-8, doi: 10.1016/j.icarus.2008.09.002, 2009.





Evolution of Mercury's obliquity

Mercury has a near-zero obliquity, i.e. its spin axis is nearly perpendicular to its orbital plane. The value of the obliquity must be known precisely in order to constrain the size of the planet's core with the framework suggested by Peale (1976). Rambaux and Bois (2004) have suggested that Mercury's obliquity varies on thousand-year timescales due to planetary perturbations, potentially ruining the feasibility of Peale's experiment.

We use a Hamiltonian approach (free of energy dissipation) to study the spin-orbit evolution of Mercury subject to secular planetary perturbations. We can reproduce an obliquity evolution similar to that of Rambaux and Bois (2004) if we integrate the system with a set of initial conditions that differs from the Cassini state. However the thousand-year oscillations in the obliquity disappear if we use initial conditions corresponding to the equilibrium position of the Cassini state. This result indicates that planetary perturbations do not force short-period, large amplitude oscillations in the obliquity of Mercury.

In the absence of excitation processes on short timescales, Mercury's obliquity will remain quasi-constant, suggesting that one of the important conditions for the success of Peale's experiment is realized.

We show that interpretation of data obtained in support of this experiment will require a precise knowledge of the spin-orbit configuration, and we provide estimates for two of the critical parameters, the instantaneous Laplace plane orientation and the orbital precession rate from numerical fits to ephemeris data.

Finally we provide geometrical relationships and a scheme for identifying the correct initial conditions required in numerical integrations involving a Cassini state configuration subject to planetary perturbations.

Yseboodt, M.and Margot, J. L.,
Evolution of Mercury's Obliquity,
Icarus Volume 181, Issue 2, Pages 327-337, doi:10.1016/j.icarus.2005.11.024, 2006.